分治法，迭代与动态规划及贪心算法感悟

分治法、动态规划法和贪心算法有相似之处。 比如需要将问题定义为子问题，然后通过求解这样的子问题来解决最终的问题。 但显然两者有很大的区别。

1. 分而治之

分而治之（-and-）：将原问题定义为n个结构与原问题相似的更小的子问题； 递归地解决此类子问题，然后将结果组合起来得到原问题的解。

分而治之模式在递归的每个级别都有三个步骤：

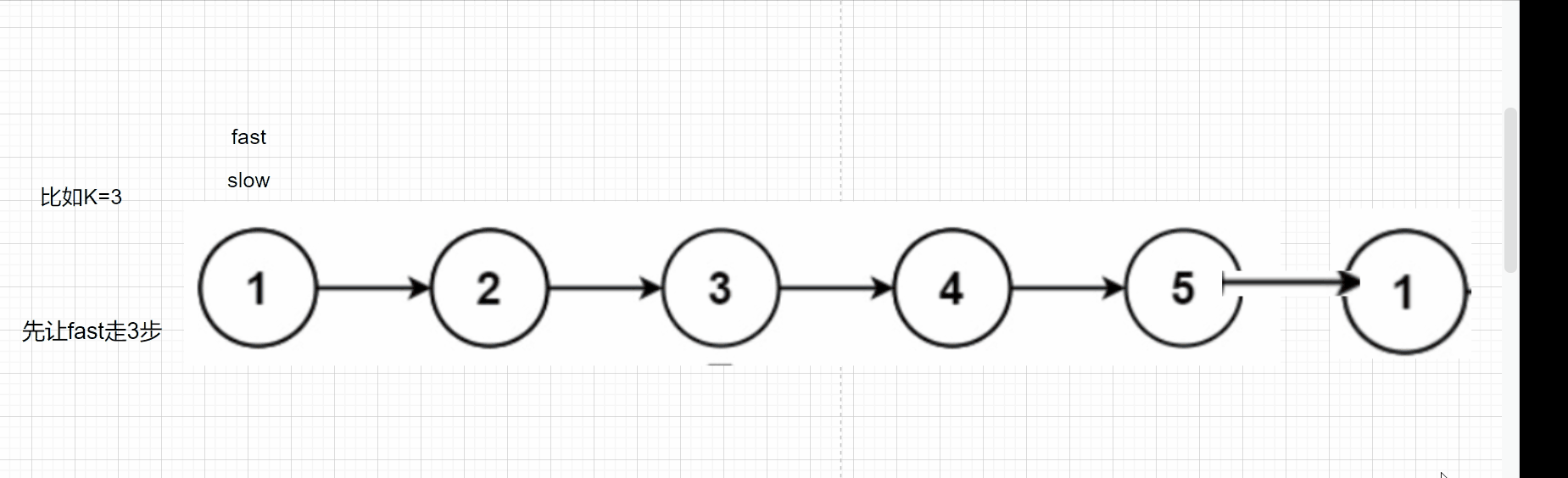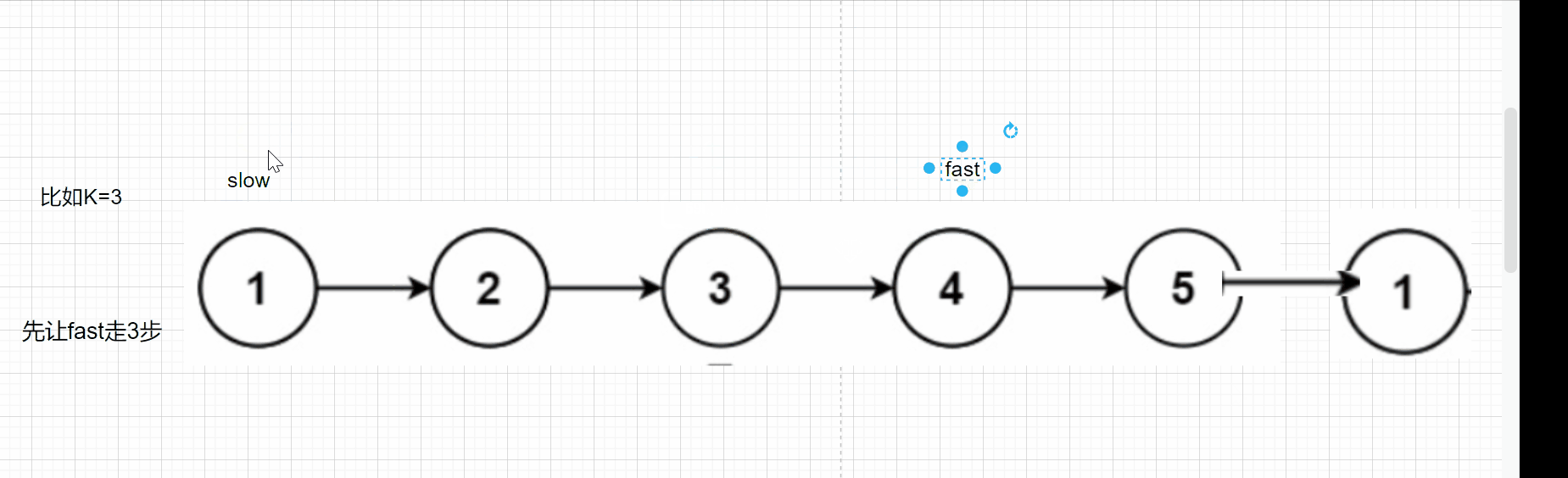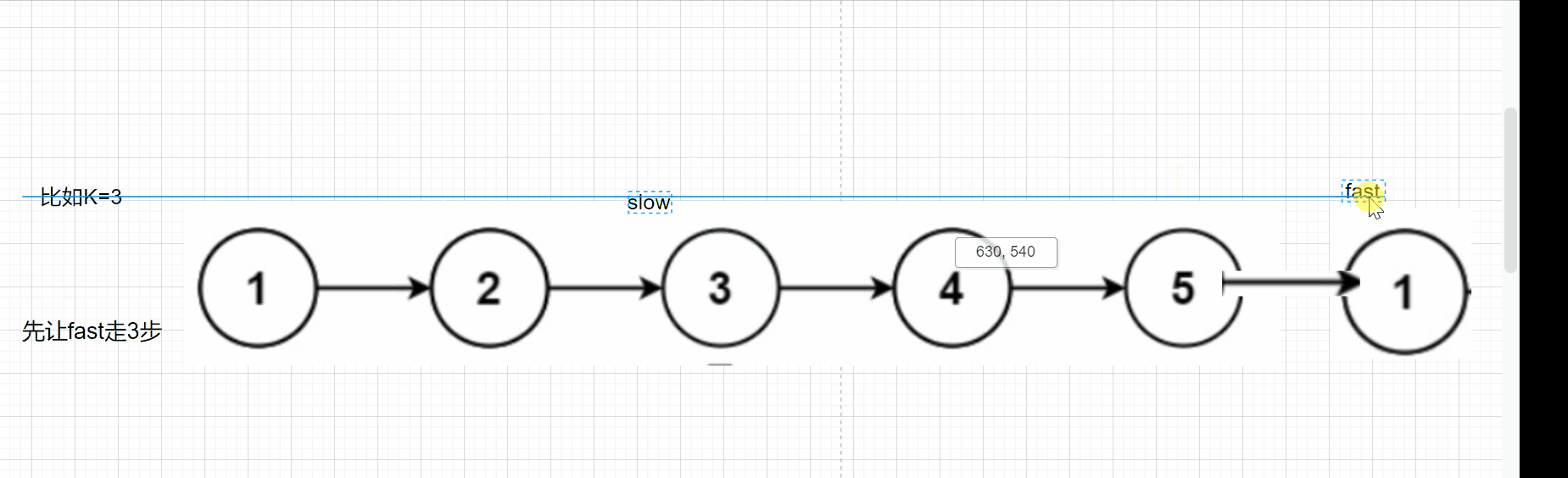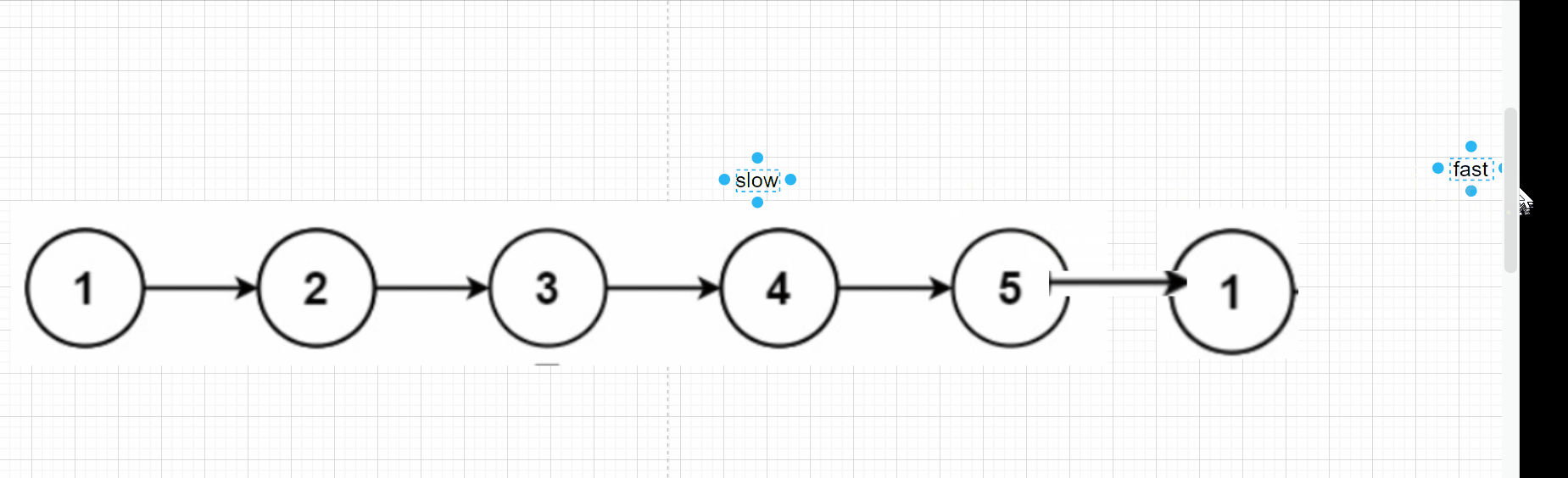
归并排序（）是分而治之的典型反例。 对应的直观操作如下：

2.动态规划法

动态规划算法的设计可以分为以下四个步骤：

分治法是指将一个问题定义为一些独立的子问题，递归求解各个子问题，然后合并子问题的解得到原问题的解。 相比之下，动态规划适用于独立和重叠的子问题，即每个子问题都包含共同的子子问题。 在这些情况下，使用分而治之的方法会做很多不必要的工作，即重复解决公共子问题。 动态规划算法对每个子子问题只求解一次，并将其结果存储在一个表中，这样就避免了每次遇到每个子问题都要重新估计答案。

适用于动态规划的优化问题中的两个要素：最优子结构和重叠子问题。

最优子结构：如果问题的最优解包含子问题的最优解，则该问题具有最优子结构。

重叠子问题：适用于动态规划的优化问题必须具备的第二个要素是子问题的空间必须很小，即用于解决原问题的递归算法重复解决相同的子问题，而不是新的子问题总是在形成。 如果两个子问题确实是同一个子问题但表现为不同问题的子问题，则它们重叠。

《分而治之：每个子问题的独立动态规划：重叠子问题》

算法简史：动态规划要求其子问题既独立又重叠，这似乎很奇怪。 事实上，这两个需求听起来可能有些矛盾，但它们描述的是两个不同的概念，而不是同一个问题的两个方面。 如果不共享资源，则同一问题的两个子问题是独立的。 如果两个子问题确实是同一个子问题但表现为不同问题的子问题，则它们重叠。

递归算法是一种通过解决同一问题的一个或多个较小实例最终解决大问题的算法。 为了在 C 中实现递归算法，经常使用递归函数，即调用自身的函数。 递归程序的基本特征：调用自身（参数值较小），有终止条件，可以直接计算结果。

在使用递归程序时，我们需要考虑到编程环境必须能够维护一个大小与递归深度成正比的下推栈。 对于小问题，这个栈所需要的空间可能会阻止我们使用递归。

递归模型是一种分而治之的方法，其最本质的特点是将一个问题分解为相互独立的子问题。 如果子问题不是独立的，问题会更复杂。 主要原因是即使是最简单的算法直接递归实现也可能需要难以想象的时间。 使用动态规划技术可以避免这种缺陷。

例如斐波那契数列的递归实现如下：

intF(inti)

{

如果（我<1）0；

如果（我==1）1；

F(i-1)+F(i-2);

}

永远不要使用这样的程序，因为它效率极低并且需要指数时间。 相反，如果首先估计前 N 个斐波那契数并将其存储在链表中，则可以在线性时间内估计 F（与 N 成反比）。

F[0]=0；F[1]=1；

对于（i=2；i1）t=F（i-1）+F（i-2）；

[i]=t;

}

性质：动态规划增加了递归函数的运行时间，即减少了估计所有大于或等于给定参数的递归调用所需的时间，其中处理递归调用的时间是常数。

我们不需要将递归参数限制为单个整数参数的情况。 当具有多个整数参数的函数时，可以将较小的子问题的解存储在多维域中，一个参数对应域的一维。 对于其他根本不涉及整形参数的情况，使用具体的离散问题公式，这使我们能够将问题分解为小问题。

在顶上动态规划中，我们存储已知值； 在自下而上的动态规划中，我们预先估计这些值。 我们经常选择自上而下的动态规划而不是自下而下的动态规划天龙八部sf，原因如下：

1 Top-up 动态规划是解决问题的自然机械转换。

2 估计子问题的顺序可以自行处理。

3 我们可能不需要估计所有子问题的解。

当我们需要的可能函数值的数量太大而无法存储（自上而下）或预先估计（自下而下）所有值时，我们不能忽视动态规划效率低下的关键点。 Top-up 动态规划确实是开发递归算法高效实现的基本技术，应该包含在算法设计和实现所需的任何工具箱中。

3.贪心算法

对于很多优化问题，使用动态规划来确定最佳选择有点“杀鸡用牛刀”天龙私服，只要采用其他更简单有效的算法即可。 贪心算法就是让做出的选择看起来是目前最好的，并期望通过做出的局部最优选择形成全局最优解。 贪心算法为大多数优化问题形成最优解，但并非总是如此。

贪心算法只需要考虑一个选择（也称为贪心选择）； 在进行贪心选择时，其中一个子问题必须为空，因此只剩下一个非空子问题。

贪心算法和动态规划有很多相似之处。 很多时候贪心法与动态规划方法的异点，贪心算法适用的问题也是一个最优子结构。 贪心算法与动态规划有一个明显的区别，即贪心算法以自上而下的方式使用最优子结构。 贪心算法会先做一个选择，看起来是当时的最优选择，然后再求解一个结果子问题，而不是先找到子问题的最优解，再做选择。

贪心算法就是通过一系列的选择，给出问题的最优解。 对于算法中的每个决策点，做出当时看起来最好的选择。 这就是贪心算法不同于动态规划的地方。 在动态规划中，每一步都会做出选择，而这种选择取决于子问题的解决方案。 出于这个原因，解决动态规划问题通常是自下而上的，从小的子问题到大的子问题。 贪婪算法做出的当前选择可能取决于所有已经做出的选择，但不取决于尚未做出的选择或子问题的解决方案。 出于这个原因，贪心算法通常会自上而下地做出贪心选择，不断将给定的问题实例缩小为更小的问题。 贪心算法定义子问题的结果，一般只有一个非空子问题。

原来的：